Container With Most Water

jidibinlin included in leetcode interval-scheduling

2022-10-04 277 words 2 minutes views

Contents

1 Description

https://leetcode-cn.com/problems/container-with-most-water/

2.analyze problem

这道题的核心是双指针和贪心算法，通过不断移动两个指针，找到局部最优解，如果局部最优解优于全局最优解，则刷新全局最优解。

2.1 slove step

分配两个指针，分别指向数组的头尾

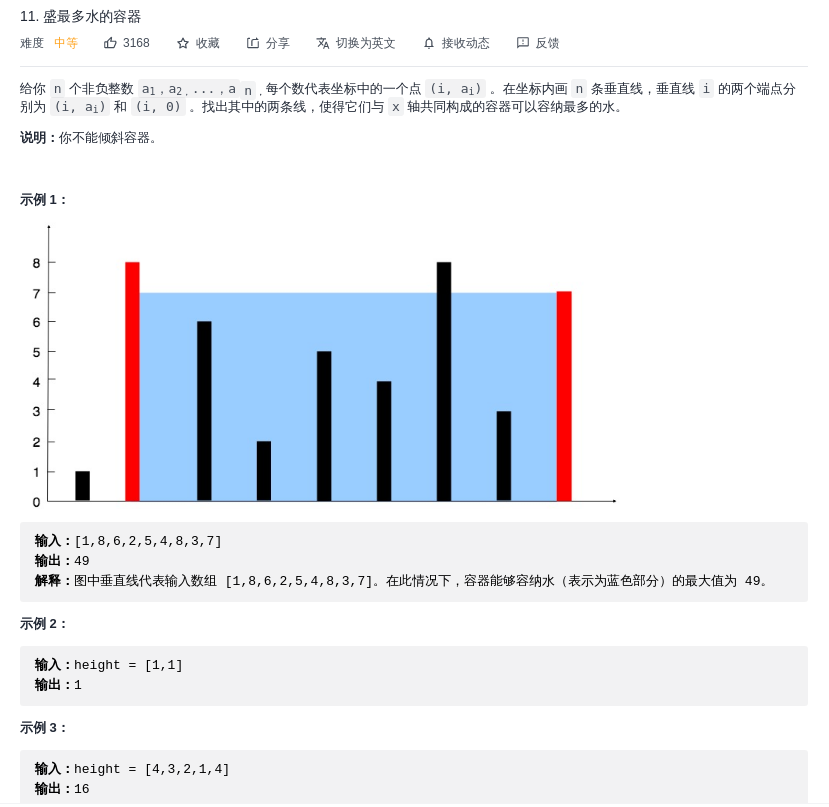
1
2


[1,8,6,2,5,4,8,3,7]
 l               r

计算面积并与全局最优解做比较，如果大于全局最优解，刷新全局最优解。并且移动对应数字较小的那个指针(向对应数字较大的方向移动)
1 2

[1,8,6,2,5,4,8,3,7] l r
重复上述操作直到指针相遇

2.2 certify

需要该解法需要证明的是，为什么每次移动对应值较小的指针是正确的。

双指针代表的是 可以作为容器边界的所有位置的范围 移动指针就代表这个指针不可能再作为容器的边界了。 为什么指向较小值的指针不可能再作为容器的边界了 。假设当前左指针和右指针指向的数分别为\(x\) 和\(y\), 不失一般性，我们假设 \(x \leq y\) 两个指针之间的距离为t。那么，他们组成的容器的容量为：

\begin{equation} \min(x,y)*t = x*t \end{equation}

如果我们保持左指针的位置不变，那么无论右指针在哪里，这个容器的容量都不会超过\(x*t\) 。为什么呢，这里我们只考虑当指针还指向左右边界的时候。我们任意向左移动右指针，指向的数为 \(y_{1}\) ，两个指针之间的距离为 \(t_{1}\) ，\(t_{1} < t\) ，并且\(min(x,y_{1}) \le min(x,y)\)

如果 \(y_{1} \le y\), then \(min(x,y_{1}) \le min(x,y)\) ;
如果 \(y_{1} \ge y\), then \(min(x,y_{1}) =x= min(x,y)\) ;

所以有

\begin{equation} \min(x,y_{t})*t_{1} < min(x,y)*t \end{equation}

这表明指向较小值的指针不可以再作为容器的边界，因为无论如何移动较大的指针，容器的容量都不会再变大。这个边界应该被舍弃。

3 implementation

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


//c++ version
#include <algrothim>
#include <iostream>
#include <math>

using namespace std;

class Solution {
public:
    int maxArea(vector<int> &height) {
        int left = 0;
        int right = height.size()-1;
        int compacity = 0;

        while (left < right) {
            int min = fmin(height[left], height[right]);
            int length = right - left;
            int tmpCompacity = min * length;

            if (tmpCompacity >= compacity)
                compacity = tmpCompacity;
            if (height[left] >= height[right])
                right--;
            else
                left++;
        }

        return compacity;
    }
};

int main(int argc, char *argv[]) { return 0; }

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


//go version
import "math"
func maxArea(height []int) int {
    front := 0
    end := len(height)-1

    var maxCompacity float64 = 0

    for front < end {
        longSide := math.Min(float64(height[front]),float64(height[end]))
        shotSide := float64(end-front)
        tmpCompacity := longSide*shotSide
        maxCompacity = math.Max(tmpCompacity,maxCompacity)
        if height[front] >= height[end] {
            end--
        }else{
            front++
        }
    }
    return int(maxCompacity)
}

4 summery

这道题用到了双指针+贪心算法。以后都可以用双指针对撞的思想去求解这类问题，重点在于如何找到应该移动的指针。当因子分布再数组的两边的时候，可以考虑使用双指针的方法求解。这题的贪心并不明显，只在更新最大的容量的时候进行了贪心。贪心的思想是每一步只选择当前认为的最优解。